【算法题】一道亚马逊面试题的情景分析
题目
亚马逊是一家纳斯达克上市公司,通过其财报我们可以解读它在给定时期内的股票走势信息。这些信息包括每天交易的最高价、最低价以及开盘价。假定你作为交易员,必须在股票开盘时做出买入或卖出的决定。你负责设计一个算法,根据给定的股价走势信息,决定买入和卖出策略,该策略必须保证你的交易获得的利润最大化。另外,股票价格的数据形式是整型数组,分别用变量 L、H、S 来代表股价在交易日的最低价、最高价和开盘价。
分析
根据题意要求,只能在开盘时做出交易决定,因此在 3 种数据中,我们只需考虑和处理数组 S。
有一个小技巧叫做具象化思考,也就是列举出一些具体的实例,这样才能有利于思考和推导。因此,我们可以假定一些具体的股票开盘价数值,看是否能通过具体的数值推导出内在规律。如下图所示,假设 S 数组中含有以下 9 个数值。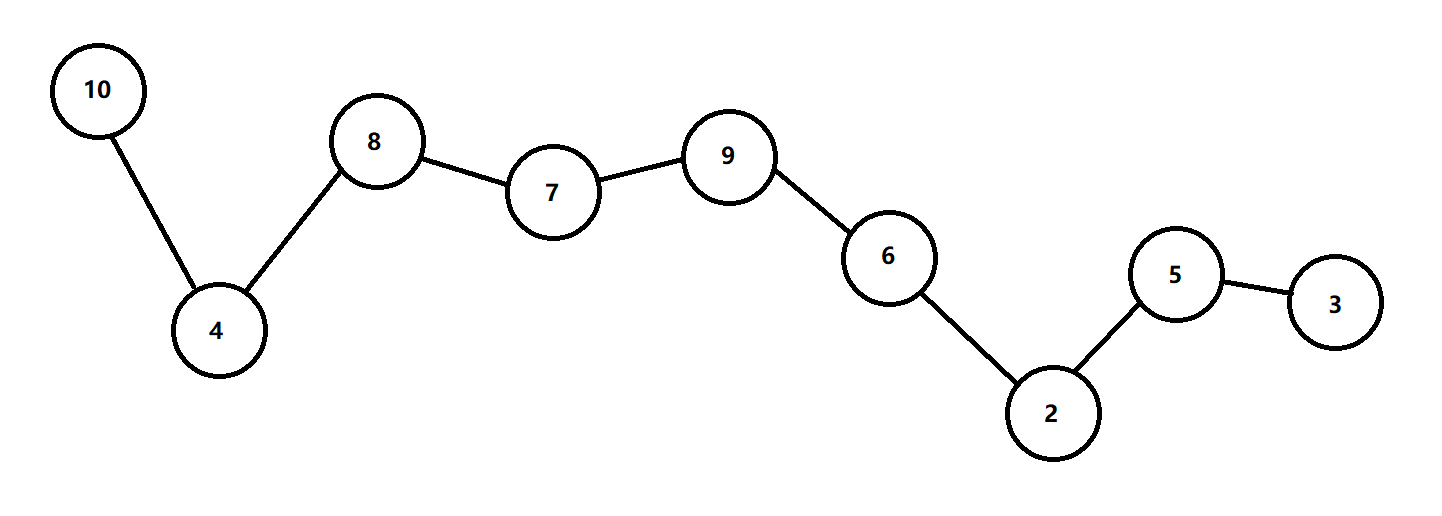
根据图示,开盘价最高点是 10,最低点是 2,我们一开始如果贸然下结论认为结果就是用最高值减去最低值,就会得到 8=10-2。但这样的话就违反了题目要求,因为必须要先买入后才能卖出。由于 10 排在 2 前面,这意味着要以 10 块钱买入,然后以 2 块钱卖出,因此这样的做法相当于亏损 8 块钱。这时可以换一种思路,使用暴力枚举法。
暴力枚举法
暴力枚举法,也就是检测任何一种可能的买卖组合。例如,第 i 天买进,第 j 天卖出,其中 j>i,计算两者间差价 P(i, j) = S[j] - S[i],并返回计算得到的最大值。由此可以得出如下代码:
# S定义股票开盘价数组
S = [10, 4, 8, 7, 9, 6, 2, 5, 3]
maxProfit = 0
buyDay = 0
sellDay = 0
for i in range(len(S) - 1):
for j in range(i+1, len(S)):
if S[j] - S[i] > maxProfit:
maxProfit = S[j] - S[i]
buyDay = i
sellDay = j
print("应该在第{0}天买入,第{1}天卖出,最大交易利润为:{2}".format(buyDay+1, sellDay+1, maxProfit))
运行后结果如下:
应该在第2天买入,第5天卖出,最大交易利润为:5
我们来分析以下算法的时间复杂度。假定数组 S 的长度为 n,上面代码有两个循环,外层循环走 n-1 次,内层循环走 n-i-1 次,因此算法的时间复杂度为:
$$\sum_{i=0}^{n-2}(n-i-1)=n(n-1)/2$$
也就是说暴力枚举法的算法复杂度为 $O(n^2)$。




不明觉厉
不错,不错
这个必须点赞👍