利用生成器解决八皇后问题

问题介绍

八皇后问题是一个以国际象棋为背景的问题：如何能够在 8x8 的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇后？为了达到此目的，任何两个皇后都不能处于同一条横线、竖线或对角线上

解决方法

状态表示

可以简单地使用元组或列表来表示可能的解（或其一部分），其中每个元素表示与这个元素索引相对应的行中皇后所在的位置（即列）。因此，如果 state[0] == 3，就说明第 1 行的皇后放在第 4 列（Python 从 0 开始计数）。在特定的行，只知道上面各皇后的位置，因此状态元组的长度小于 8。举个例子，如果前面 7 个皇后已经放置完毕，那么对于第 8 个皇后来说，它的其中一个状态元组如下所示：(0, 4, 7, 5, 2, 6, 1)

检测冲突

要找出没有冲突（即任何一个皇后都吃不到其他皇后）的位置组合，首先必须定义冲突是什么。我们使用一个函数 conflict 来定义给定下一个皇后的位置 nextX，判断其是否与之前的每个皇后产生冲突：

def conflict(state, nextX):
    nextY = len(state)
    for i in range(nextY):
        if abs(state[i] - nextX) in (0, nextY - i):
            return True
    return False

参数 state 表示当前皇后的状态元组，nextX 表示当前皇后的水平位置（x 坐标，即列），而 nextY 为当前皇后的垂直位置（y 坐标，即行）。这个函数对之前的每个皇后执行简单的检查：如果当前皇后与之前某个皇后的列相同或在同一条对角线上，将发生冲突，因此函数返回 True；如果与之前每一个皇后都没发生冲突，就返回 False。

比较难理解的是这个表达式：

abs(state[i] - nextX) == nextY - i

两个皇后的水平位置的距离等于垂直位置的距离，就说明这两个皇后在一条对角线上。

基线条件

使用生成器可以较为简单地解决八皇后问题，但是这个方案的效率不是特别高，因此皇后非常多时，速度会比较慢。

下面先来看基线条件：最后一个皇后。假设在给定了前面所有皇后的位置下，对于最后一个皇后，为了找出所有可能的解（当然也可能什么位置都不行），可以像下面这样编写代码：

def queens(num, state):
    if len(state) == num - 1:
        for pos in range(num):
            if not conflict(state, pos):
                yield pos

这段代码的意思是，如果只剩下最后一个皇后没有放好，就遍历所有可能的位置，并返回那些不会引发冲突的位置。参数 num 为皇后总数，而参数 state 是一个元组，包含已放好的皇后位置。例如，假设共有 4 个皇后，而前 3 个皇后的位置分别为 1、3 和 0，如下图所示（红色的皇后为最终解，现在不用关心）：

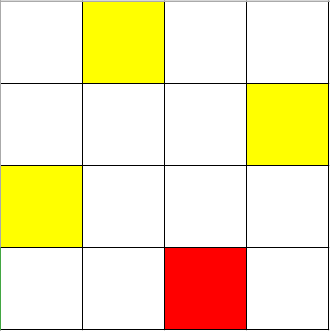
从该图可知，每个皇后都占据一行，而皇后的位置是从 0 开始编号的。

>>> list(queens(4, (1, 3, 0)))
[2]

代码的效果很好。这里使用 list 旨在让生成器生成所有的值。在这个示例中，只有一个位置符合条件。

递归条件

现在来看看这个解决方案的递归部分。处理好基线条件后，可在递归条件中假设来自更低层级（编号更大的皇后）的结果都是正确的。因此，只需在函数 queens 的前述实现中给 if 语句添加一个 else 子句。

我们希望递归调用接收由当前行上面的皇后位置组成的元组，对于当前皇后的每个合法位置，返回由当前皇后位置加上当前行下面的皇后位置组成的元组。假设位置是以元组的方式返回的，因此需要修改基线条件，使其返回一个（长度为 1 的）元组。为了让这个过程不断进行下去，只需将当前皇后的位置插入到返回的结果开头，如下所示：

def queens(num, state):
    if len(state) == num - 1:
        for pos in range(num):
            if not conflict(state, pos):
                yield (pos,)
    else:
        for pos in range(num):
            if not conflict(state, pos):
                for result in queens(num, state + (pos,)):
                    yield (pos,) + result

这里的 for pos 和 if not conflict 部分与前面相同，因此可以稍微简化一下代码。另外，还可以给参数指定默认值。

def queens(num=8, state=()):
    for pos in range(num):
        if not conflict(state, pos):
            if len(state) == num - 1:    
                yield (pos,)
            else:
                for result in queens(num, state + (pos,)):
                    yield (pos,) + result

其中，(pos,) 中的逗号必不可少，这样得到的才是元组。

生成器 queens 提供了所有的解，一共 92 个。

>>> list(queens(3))
[]
>>> list(queens(4))
[(1, 3, 0, 2), (2, 0, 3, 1)]
>>> for solution in queens(8):
...     print(solution)
...
(0, 4, 7, 5, 2, 6, 1, 3)
(0, 5, 7, 2, 6, 3, 1, 4)
...
(7, 2, 0, 5, 1, 4, 6, 3)
(7, 3, 0, 2, 5, 1, 6, 4)
>>> len(list(queens(8)))
92

扫尾工作

在结束之前，可以让输出更容易理解些。在任何情况下，清晰的输出都是好事，因为这让查找 bug 等工作更容易。

def prettyprint(solution):
    def line(pos, length=len(solution)):
        return '. ' * (pos) + 'O ' + '. ' * (length-pos-1)
    for pos in solution:
        print(line(pos))

请注意，我在 prettyprint 中创建了一个简单的辅助函数。之所以将它放在 prettyprint 中，是因为我认为在其他地方都用不到它。下面随机地选择一个解，并将其打印出来，以确定它是正确的。

>>> import random
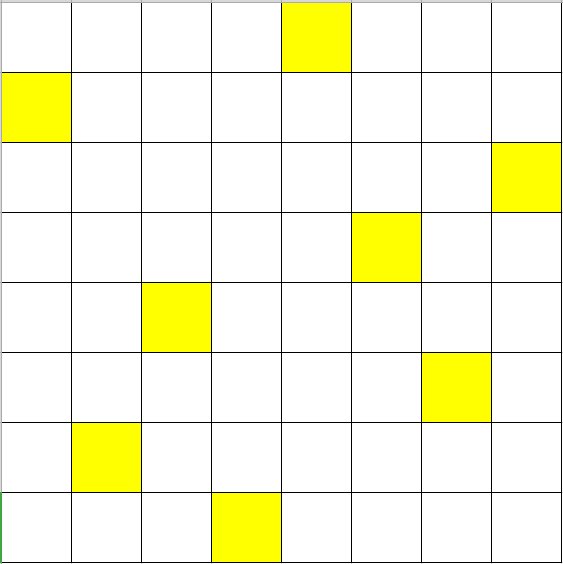
>>> prettyprint(random.choice(list(queens(8))))
. . . . O . . .
O . . . . . . .
. . . . . . . O
. . . . . O . .
. . O . . . . .
. . . . . . O .
. O . . . . . .
. . . O . . . .

下图显示了这个解。