【数据结构与算法】遗传算法(二)定义
1、遗传算法定义
首先我们回到前面讨论的那个例子,并总结一下我们做过的事情。
-
首先,我们设定好了国民的初始人群大小。
-
然后,我们定义了一个函数,用它来区分好人和坏人。
-
再次,我们选择出好人,并让他们繁殖自己的后代。
-
最后,这些后代们从原来的国民中替代了部分坏人,并不断重复这一过程。
遗传算法实际上就是这样工作的,也就是说,它基本上尽力地在某种程度上模拟进化的过程。
因此,为了形式化定义一个遗传算法,我们可以将它看作一个优化方法,它可以尝试找出某些输入,凭借这些输入我们便可以得到最佳的输出值或者是结果。遗传算法的工作方式也源自于生物学,具体流程见下图: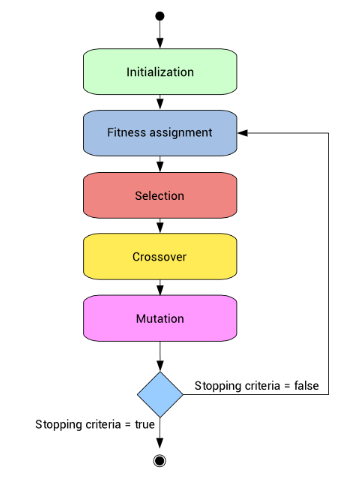
2、遗传算法具体步骤
为了让讲解更为简便,我们先来理解一下著名的组合优化问题「背包问题」。如果你还不太懂,这里有一个我的解释版本。
比如,你准备要去野游 1 个月,但是你只能背一个限重 30 公斤的背包。现在你有不同的必需物品,它们每一个都有自己的「生存点数」(具体在下表中已给出)。因此,你的目标是在有限的背包重量下,最大化你的「生存点数」。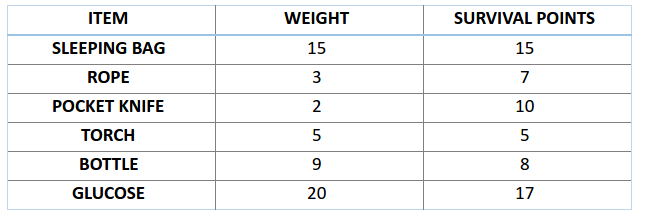
2.1 初始化
这里我们用遗传算法来解决这个背包问题。第一步是定义我们的总体。总体中包含了个体,每个个体都有一套自己的染色体。
我们知道,染色体可表达为二进制数串,在这个问题中,1 代表接下来位置的基因存在,0 意味着丢失。(译者注:作者这里借用染色体、基因来解决前面的背包问题,所以特定位置上的基因代表了上方背包问题表格中的物品,比如第一个位置上是 Sleeping Bag,那么此时反映在染色体的『基因』位置就是该染色体的第一个『基因』。)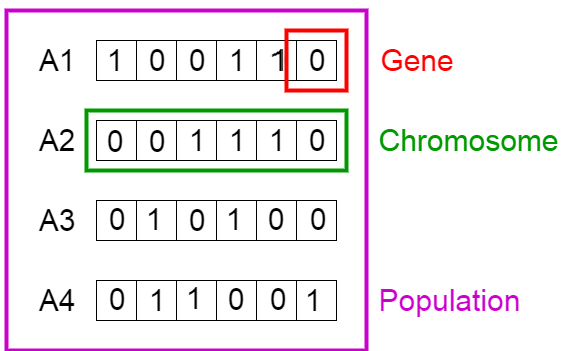
现在,我们将图中的 4 条染色体看作我们的总体初始值。
2.2 适应度函数
接下来,让我们来计算一下前两条染色体的适应度分数。对于 A1 染色体 [100110] 而言,有: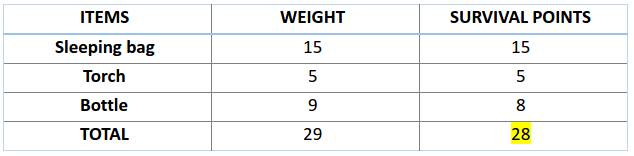
类似地,对于 A2 染色体 [001110] 来说,有: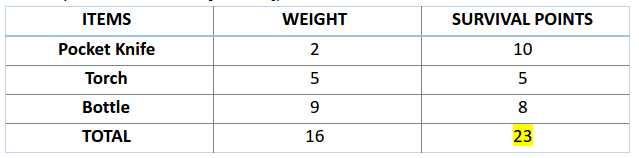
对于这个问题,我们认为,当染色体包含更多生存分数时,也就意味着它的适应性更强。
因此,由图可知,染色体 1 适应性强于染色体 2。
2.3 选择
现在,我们可以开始从总体中选择适合的染色体,来让它们互相『交配』,产生自己的下一代了。这个是进行选择操作的大致想法,但是这样将会导致染色体在几代之后相互差异减小,失去了多样性。因此,我们一般会进行「轮盘赌选择法」(Roulette Wheel Selection method)。
想象有一个轮盘,现在我们将它分割成 m 个部分,这里的 m 代表我们总体中染色体的个数。每条染色体在轮盘上占有的区域面积将根据适应度分数成比例表达出来。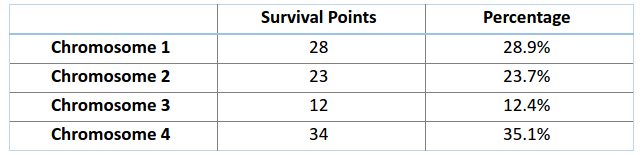
基于上图中的值,我们建立如下「轮盘」。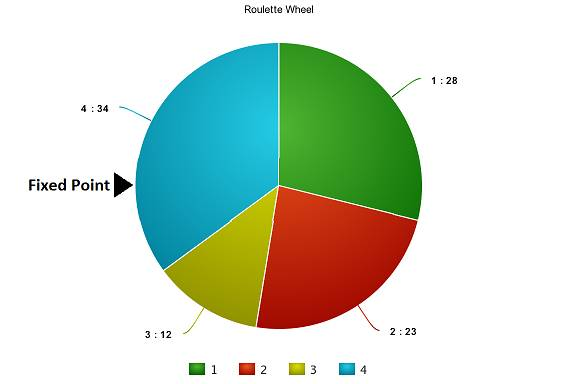
现在,这个轮盘开始旋转,我们将被图中固定的指针(fixed point)指到的那片区域选为第一个亲本。然后,对于第二个亲本,我们进行同样的操作。有时候我们也会在途中标注两个固定指针,如下图: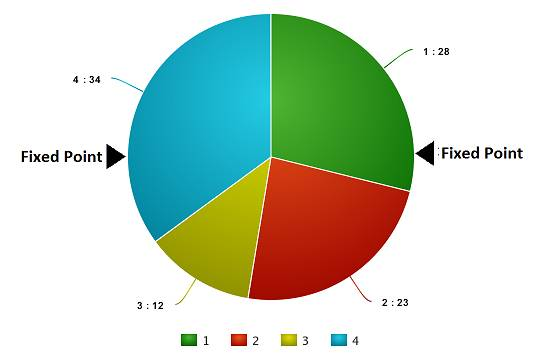
通过这种方法,我们可以在一轮中就获得两个亲本。我们将这种方法成为「随机普遍选择法」(Stochastic Universal Selection method)。
2.4 交叉
在上一个步骤中,我们已经选择出了可以产生后代的亲本染色体。那么用生物学的话说,所谓「交叉」,其实就是指的繁殖。现在我们来对染色体 1 和 4(在上一个步骤中选出来的)进行「交叉」,见下图: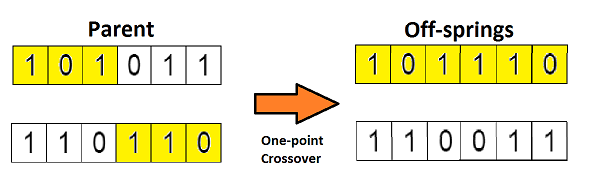
这是交叉最基本的形式,我们称其为「单点交叉」。这里我们随机选择一个交叉点,然后,将交叉点前后的染色体部分进行染色体间的交叉对调,于是就产生了新的后代。
如果你设置两个交叉点,那么这种方法被成为「多点交叉」,见下图: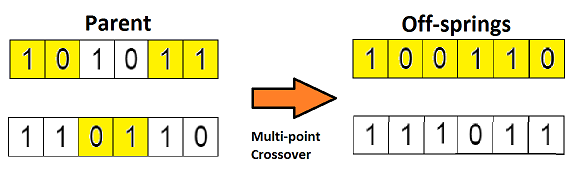
2.5 变异
如果现在我们从生物学的角度来看这个问题,那么请问:由上述过程产生的后代是否有和其父母一样的性状呢?答案是否。在后代的生长过程中,它们体内的基因会发生一些变化,使得它们与父母不同。这个过程我们称为「变异」,它可以被定义为染色体上发生的随机变化,正是因为变异,种群中才会存在多样性。
下图为变异的一个简单示例:
变异完成之后,我们就得到了新为个体,进化也就完成了,整个过程如下图: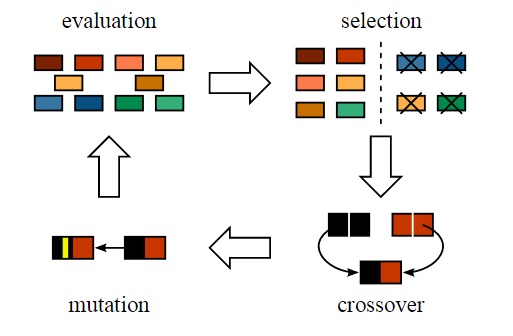
在进行完一轮「遗传变异」之后,我们用适应度函数对这些新的后代进行验证,如果函数判定它们适应度足够,那么就会用它们从总体中替代掉那些适应度不够的染色体。这里有个问题,我们最终应该以什么标准来判断后代达到了最佳适应度水平呢?
一般来说,有如下几个终止条件:
-
在进行 X 次迭代之后,总体没有什么太大改变。
-
我们事先为算法定义好了进化的次数。
-
当我们的适应度函数已经达到了预先定义的值。