【算法题】汉诺塔问题
《从一到无穷大》一书中提到一个关于“世界末日”的问题。爱好数学的历史学家 W.W.R. 鲍尔(W.W.W.R. Ball)是这样说的:
在贝拿勒斯那座伟大的神庙里,代表世界中心的穹顶之下安放着一块铜板,铜板上镶有 3 根高 1 腕尺(约等于 20 英寸)、蜜蜂身体一般粗的金刚石针。神在创世时将 64 张纯金圆片安放在其中一根针上,最大的金片直接放置在铜板上,其余金片依次堆叠,逐渐缩小,这就是梵塔。值守的僧侣夜以继日、从不停歇地将这些金片从一根金刚石针转移到另一根金刚石针上。至于梵塔如何转移,神定下了不可更改的铁律:僧侣每次只能移动一张金片,所有金片必须安放在金刚石针上,较小的金片绝不能放在比它大的金片下面。等到全部 64 张金片都从创世时神安放的那根针转移到另一根针上面,塔、神庙和婆罗门都将化为尘埃,世界也将在轰鸣的霹雳中归于寂灭。
汉诺塔问题不管在任何编程语言里都是经典问题,是采用递归算法的经典案例,该问题可以抽象如下:
- 3 根圆柱 A,B,C,其中 A 上面串了 n 个圆盘
- 这些圆盘从上到下是按从小到大顺序排列的,大的圆盘任何时刻不得位于小的圆盘上面
- 每次移动一个圆盘,最终实现将所有圆盘移动到C上
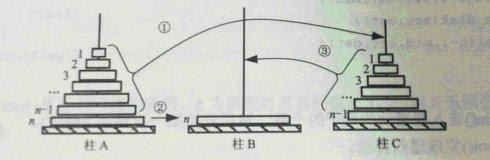
利用 Python 语言接近自然语言的特性,可以更容易的将递归算法翻译成程序语句,需要的代码量很小。汉诺塔问题的解决步骤用语言描述很简单,仅三步:
A,B,C 三个圆柱,分别为初始位,过渡位,目标位,设 A 柱为初始位,C 位为最终目标位
(1)将最上面的 n-1 个圆盘从初始位移动到过渡位
(2)将初始位的最底下的一个圆盘移动到目标位
(3)将过渡位的 n-1 个圆盘移动到目标位
对于递归算法中的嵌套函数 f(n-1)来说,其初始位,过渡位,目标位发生了变化
完整代码如下:
def destory(n, begin='A', middle='B', end='C'):
if n == 1:
print('{}-->{}'.format(begin, end))
elif n == 2:
print('{}-->{}'.format(begin, middle))
print('{}-->{}'.format(begin, end))
print('{}-->{}'.format(middle, end))
else:
destory(n-1, begin='A', middle='C', end='B')
print('A-->C')
destory(n-1, begin='B', middle='A', end='C')